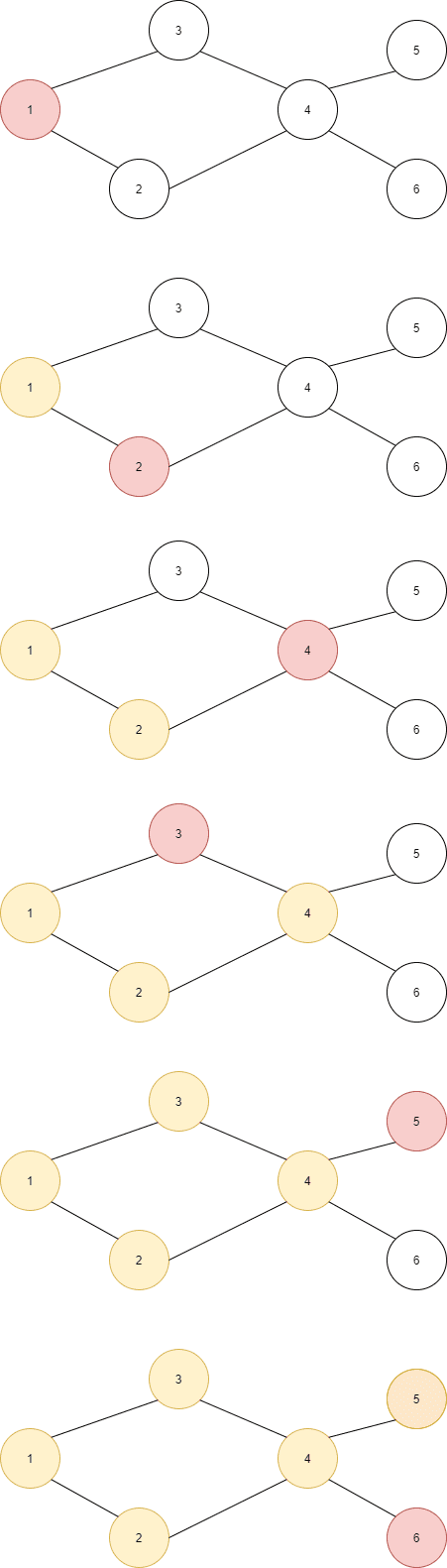
DFS
그래프의 모든 정점를 순회하는 고전적인 방법 중 하나는 DFS(Depth First Search)이다.
현재 정점과 인접한 간선들을 검사하면서 아직 방문하지 않은 정점이라면 바로 방문하고,
더 이상 방문 가능한 정점이 없다면 이전에 방문한 정점으로 돌아가는 방식으로 진행된다.
각 스텝에서 붉은 색은 가장 마지막에 방문한 정점이며, 노란 색은 이미 방문한 정점을 나타낸다.
1번 정점부터 차례대로 갈 수 있는 모든 정점들을 탐색하며
3번 정점에서는 더 이상 방문할 곳이 없다.
이 때는 그 이전에 방문했던 4번 노드로 돌아와서 방문 가능한 정점들을 다시 찾는다.
DFS는 재귀 호출로 간단하게 구현할 수 있으며 인접 리스트를 사용하여 구현할 시에는 의 시간 복잡도를, 인접 행렬을 사용하여 구현할 시에는 의 시간 복잡도를 가진다.
// adjacency list
vector<vector<int> > adj;
vector<bool> visited;
void dfs(int here){
cout << "VISIT : " << here << endl;
visited[here] = true;
// 모든 정점을 순회하며 방문 가능한 정점으로 간다.
for(int i = 0 ; i < adj[here].size() ; i++){
int there = ajd[here][i];
if(!visited[there]) dfs(there);
}
// 재귀 호출에 걸리지 않고 여기까지 현재 노드에서 더 이상 방문 가능한 곳이 없음.
}
// 만약 그래프가 둘 이상의 그룹
// 즉, 서로 연결되지 않은 부분 집합으로 나누어져있다면 아래와 같이 구현해서 모든 정점을 확인한다.
void dfsAll(){
visited = vector<bool>(adj.size(), false);
for(int i = 0 ; i < adj.size() ; i++){
if(!visited[i]) dfs(i);
}
}BFS
그래프 순회에 있어 다른 방법은 BFS(Breadth First Search)가 있다.
시작 정점에서 방문 가능한 가까운 정점부터 방문하는 방식이다.
먼저 시작 정점에서 방문 가능한 곳을 모든 정점을 검사하며,
연결된 정점을 방문 예정이라고 기록하여 별도 위치에 저장해둔다.
그리고 현재 정점의 검사가 끝나면 저장해둔 목록에서 하나를 꺼내 다음 정점을 방문한다.
각 스텝에서 붉은 색은 가장 마지막에 방문한 정점이며, 노란 색은 이미 방문한 정점을 나타낸다.
BFS는 Queue를 사용하여 구현할 수 있으며 인접 리스트를 사용하여 구현할 시에는 의 시간 복잡도를, 인접 행렬을 사용하여 구현할 시에는 의 시간 복잡도를 가진다.
// adjacency list
vector<vector<int> > adj;
vector<int> bfs(int start){
// 방문 여부
vector<bool> visited(adj.size(), false);
// 방문 예정 정점 저장
queue<int> q;
// 방문 순서 기록
vector<int> order;
visited[start] = true;
q.push(start);
while(!q.empty()){
int here = q.front();
q.pop();
order.push_back(here);
// 연결된 정점 검사
for(int i = 0 ; i < adj[here].size() ; i++){
int there = adj[here][i];
if(!visited[there]){
q.push(there);
visited[there] = true;
}
}
}
return order;
}참고
- 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략