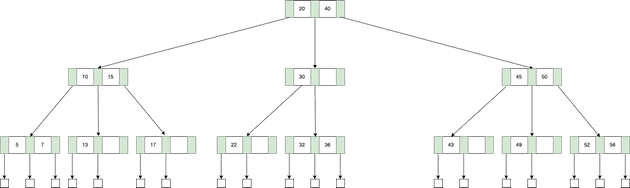
어떤 연산을 진행할 때, 산술이나 논리 연산이 동작하는 시간보다 비교할 수 없을 정도로 많은 시간을 잡아 먹는 것이 디스크나 메모리 접근이다. AVL Tree나 Red-Black Tree는 노드 하나가 몇 바이트밖에 되지 않기 때문에 디스크 블록과 같은 큰 단위를 효율적으로 사용할 수 없다. B-Tree는 연산의 수는 증가할지 모르지만, 디스크 접근을 줄이기 위해 높이를 줄이는 방식을 선택한다. 하나의 노드가 여러 개의 키를 가지고 자식들을 가지며, 보통 하나의 캐시 라인이나 디스크 블록을 채울 수 있는 가장 큰 차수를 사용한다. 많은 데이터베이스에서 인덱스를 표현하는 구조로 채택하고 있는 자료구조이기도 하다. 아래는 3차 B-Tree의 예시이다.
M-Way(Multiway) Search Tree
B-Tree의 더 상위 개념은 하나의 노드에 여러 개의 키가 할당될 수 있는 M-Way(Multiway) Search Tree이며 그 특징은 아래와 같다.
각 노드는 최대 M개의 자식, M-1개의 키를 가질 수 있다
만약 M=3이라면 이를 3차 트리라고 한다. 그리고 자식의 개수가 K이면, 키의 개수는 K-1개여야 한다.
노드 내부 키 값들은 정렬되어 있다
각 노드의 키 값들은 정렬되어 있으며 여기에는 자식 트리의 값들 까지 포함한다. 예를 들어, K번 째 값은 K번 째 자식 트리 내부의 모든 값 보다 크고, K+1번 째 자식 트리의 모든 값보다 작다.
B-Tree
B-Tree를 만족하기 위해서는 아래와 같은 특징을 가져야 한다.
모든 외부 노드의 레벨은 같다
n(키의 값 수) >= 0이고, m > 2 일 때 B-Tree는 항상 존재한다. 하지만, m=2(2차 B-Tree) 같은 경우는 조건을 만족하기 위해 항상 Full Binary Tree를 만족해야 한다. 즉, 키의 수가 개 일 때만 성립할 수 있다.
External node는 탐색 중에 트리에서 찾고자 하는 원소를 찾지 못했을 때 도달하는 노드를 의미하며 실제 구현에서는 nullptr을 의미한다.
루트 노드는 최소 2개의 자식을 가지며, 모든 노드는 최소 M/2개의 자식을 가진다
M차 B-Tree의 외부 노드들의 레벨이 이라면, 키의 수는 최대 개가 된다. 그렇다면 키의 최소 개수는 어떻게 될까? 전제 조건에 따르면 루트 노드는 최소 2개의 자식을 가지고, 각 노드는 개의 자식을 가지므로 level 3에서는 최소 개의 노드가 나타난다. 이를 더 일반화하면 level l에서는 개의 nonfailure node를 가진다. 그리고 키의 개수를 이라고 할 때, failure node의 개수는 이 되며, 이는 level에 위치한다.
이고 이라고 했을 때, l은 3 이하의 값을 가진다. 실질적으로는 노드 하나를 탐색하는데 있어, 한 번의 메모리 접근을 하도록 구성한다. 메인 메모리를 대상으로는 그 크기가 보통 수십, 디스크 대상으로는 수백으로 구성된다.
노드 탐색
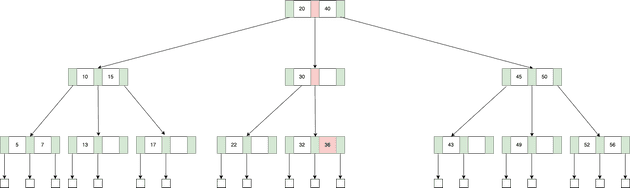
B-Tree의 형태를 이해한다면, 탐색 과정은 직관적으로 이루어진다. 36이라는 값을 찾아보자.
- 루트 노드에서 20~40 사이의 값을 가지므로 중간 서브 트리로 넘어간다.
- 30보다 큰 값을 가지므로 오른쪽 서브 트리로 넘어간다.
- 선형 탐색 결과 36이 존재하며 탐색이 완료된다.
노드 삽입
- 삽입 가능한 적절한 위치가 존재하는 경우
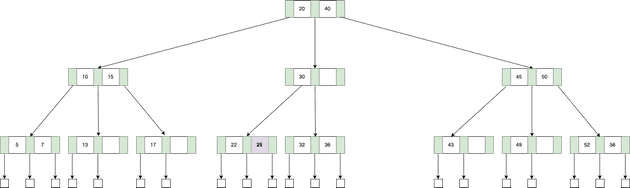
25의 값을 갖는 키를 삽입해보자. 위치를 탐색했을 때, 적절한 공간이 존재한다면 그냥 삽입하면 된다.
- 트리를 분할해야하는 경우
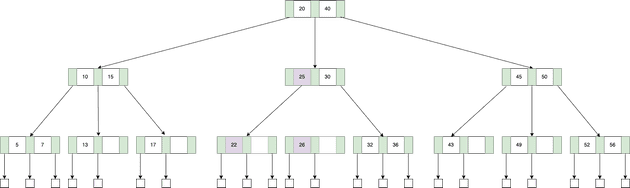
이제 이어 26의 값을 갖는 키를 삽입해보자. 위치 상 [22, 25]를 가지는 노드에 삽입되어야 하는데 이미 가득 차 있기 때문에 분할하고 새로운 노드를 생성하는 작업이 필요하다. 세 가지 값 중 가장 작은 값은 기존 노드의 위치에, 중간 값은 부모 노드에, 가장 큰 값은 새로운 노드의 원소로 삽입된다. 이 때 부모 노드에 키가 삽입되면 부모를 다시 분할해야하는 케이스가 발생할 수 있는데 그 때는 이를 재귀적으로 적용하면 된다.
참고
- Ellis Horowitz, Sartaj Sahni, Susan Anderson-Freed, Fundamentals of Data Structures in C, Pearson